2022년06월18일 17번
[과목 구분 없음] <보기>와 같이 반지름이 각각 ra, rb인 원형 도선 a, b에 각각 세기가 일정한 전류가 흐르고 있다. 점 Oa, Ob는 a와 b의 중심이며 a와 b에 흐르는 전류에 의한 자기모멘트의 크기가 같다. Oa, Ob에서 전류에 의한 자기장의 세기를 각각 Ba, Bb라고 할 때, Bb/Ba는?

-
①
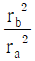
-
②
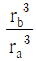
-
③
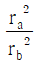
-
④

(정답률: 알수없음)
문제 해설




Ma = πra2 Ia
Mb = πrb2 Ib
여기서 Ia와 Ib는 각각 a와 b를 흐르는 전류의 세기이다.
점 Oa에서의 자기장의 세기 Ba는 다음과 같다.
Ba = μ0 Ia / (2ra)
여기서 μ0은 자유공간의 유전율이다.
점 Ob에서의 자기장의 세기 Bb는 다음과 같다.
Bb = μ0 Ib / (2rb)
따라서 Bb/Ba는 다음과 같다.
Bb/Ba = (Ib/rb) / (Ia/ra) = ra/rb
따라서 정답은 "
이유는 원형 도선 a와 b에 흐르는 전류에 의한 자기모멘트의 크기가 같으므로, 반지름이 작은 도선 a에서는 전류 밀도가 크고, 반지름이 큰 도선 b에서는 전류 밀도가 작아야 한다. 따라서 b에서의 자기장의 세기는 a에서의 자기장의 세기보다 작아야 하므로 Bb/Ba는 ra/rb보다 작아야 한다.